| Title: | Process Improvement using Data |
| Version: | 0.50 |
| Date: | 2018-11-21 |
| Author: | Kevin Dunn [aut, cre] |
| Maintainer: | Kevin Dunn <kgdunn@gmail.com> |
| Imports: | ggplot2, stats, png, FrF2, DoE.base, FrF2.catlg128 |
| Suggests: | MASS |
| Description: | A collection of scripts and data files for the statistics text: "Process Improvement using Data" https://learnche.org/pid and the online course "Experimentation for Improvement" found on Coursera. The package contains code for designed experiments, data sets and other convenience functions used in the book. |
| License: | BSD_2_clause + file LICENSE |
| URL: | https://learnche.org/pid |
| NeedsCompilation: | no |
| BugReports: | https://bitbucket.org/kevindunn/r-pid |
| RoxygenNote: | 6.1.1 |
| Packaged: | 2018-11-22 21:13:18 UTC; kevindunn |
| Repository: | CRAN |
| Date/Publication: | 2018-11-23 17:30:03 UTC |
Process Improvement using Data
Description
This package contains functions and datasets that complement the book Process Improvement using Data, https://learnche.org/pid.
The functions and datasets are also used in the massive open online course (MOOC) called "Experimentation for Improvement", hosted on Coursera, https://yint.org/experiments.
The functions are most useful for design of experiments (DOE), and additional functions and datasets will be added as the book and the MOOC evolve over time.
Details
The package is still subject to development, in terms of datasets and functionality, at least until version numbers exceed 1.0. Version numbers below 1.0 indicate that functionality may be added, removed or changed over time.
Please contact me, if you have suggestions.
Other packages that you can use immediately for experimental design are: FrF2 for fractional factorial experiments with 2-level factors and the base package for Designed Experiments, called DoE.base.
Author(s)
Kevin Dunn
Maintainer: Kevin Dunn <kgdunn@gmail.com>
References
Box G. E. P, Hunter, W. C. and Hunter, J. S. (2005) Statistics for Experimenters, 2nd edition. New York: Wiley.
See Also
Related packages: DoE.base, BsMD, FrF2
Examples
# 2-factor example
T <- c(-1, +1, -1, +1) # centered and scaled temperature
S <- c(-1, -1, +1, +1) # centered and scaled speed variable
y <- c(69, 60, 64, 53) # conversion, is our response variable, y
doe.model <- lm(y ~ T + S + T * S) # create a model with main effects, and interaction
paretoPlot(doe.model)
# 3-factor example
data(pollutant)
mod.full <- lm(y ~ C*T*S, data=pollutant)
paretoPlot(mod.full)
Full factorial experiments for stove-top boiling of water.
Description
The data are from boiling water in a pot under various conditions. The response variable,
y, is the time taken, in minutes to reach 90 degrees Celsius. Accurately measuring
the time to actual boiling is hard, hence the 90 degrees Celsius point is used instead.
Three factors are varied in a full factorial manner (the first 8 observations). The data are in standard order, however the actual experiments were run in random order. The last 3 rows are runs close to, or interior to the factorial.
Factors varied were:
-
A= Amount of water: low level was 500 mL, and high level was 600 mL -
B= Lid off (low level) or lid on (high level) -
C= Size of pot used: low level was 2 L, and high level was 3 L.
Coded values for A, B, and C, should be used in the linear
regression model analysis, with -1 representing the low value and +1 the
high value.
Usage
data(boilingpot)Format
A data.frame containing 11 observations of 4 variables (A, B, C, with y as a response variable.)
Source
A MOOC on Design of Experiments: “Experimentation for Improvement”, https://learnche.org
2-dimensional contour plot of a factorial design model
Description
Creates a two-dimensional contour plot of a factorial design model (linear least squares model). The two specified factors are plotted on the horizontal and vertical axes. If the model has more than two factors, then the remaining factors are set at their zero level. It is assumed the model is in coded units.
Usage
contourPlot(lsmodel,
xlab=attr(lsmodel$terms,'term.labels')[1],
ylab=attr(lsmodel$terms,'term.labels')[2],
main="Contour plot",
N=25,
xlim=c(-3.2, 3.2),
ylim=c(-3.2, 3.2),
colour.function=terrain.colors)Arguments
lsmodel |
a linear model object (least squares model) created by the |
xlab |
the label and variable used for horizontal axis in the bar plot, and must also match a variable in the |
ylab |
the label and variable used for vertical axis in the bar plot, and must also match a variable in the |
main |
label for the plot. |
N |
the resolution of the plot; higher values have greater resolution. |
xlim |
the limits of the horizontal axis (in coded units); the defaults indicate the model's effect outside the standard factorial range. |
ylim |
the limits of the vertical axis (in coded units); the defaults indicate the model's effect outside the standard factorial range. |
colour.function |
the function used to colour-code the contour plot; see |
Details
Typical usage is to create a generic linear model with the lm(...) command, and supply that as the input to this function.
For example, a general design of experiments with 4 factors: A, B, C, and D can be built using
lsmodel <- lm(y ~ A*B*C*D), and then various 2-D contour plots visualized with
contourPlot(lsmodel, "A", "B"), contourPlot(lsmodel, "B", "C"), or whichever combination of factors
are desired. The variables not being plotted are set at their zero (0) value.
Future versions of this function will allow specifying the inactive variable levels. In the interim, please see the rsm
package (the rsm::contour(...) function) if this functionality is required.
Value
Returns a ggplot2 object, which, by default, is shown before being returned by this function.
The ggplot2 object may be further manipulated, if desired.
Author(s)
Kevin Dunn, <kgdunn@gmail.com>
References
Please see Chapter 5 of the following book: Kevin Dunn, 2010 to 2019, Process Improvement using Data, https://learnche.org/pid
Examples
# 2-factor example
# ----------------
T <- c(-1, +1, -1, +1) # centered and scaled temperature
S <- c(-1, -1, +1, +1) # centered and scaled speed variable
y <- c(69, 60, 64, 53) # conversion, is our response variable, y
doe.model <- lm(y ~ T + S + T * S) # model with main effects, and interaction
contourPlot(doe.model)
# 3-factor example
# ----------------
data(pollutant)
mod.full <- lm(y ~ C*T*S, data=pollutant)
contourPlot(mod.full, N=50) # high resolution plot
contourPlot(mod.full, xlab='C', ylab='S',
main="Strong C:S interaction",
colour.function=rainbow)
# Central composite design
P <- c(-1, +1, -1, +1, 0, -1.41, 0, +1.41)
T <- c(-1, -1, +1, +1, +1.41, 0, -1.41, 0)
y <- c(715, 713, 733, 725, 738, 717, 721, 710)
mod.CCD <- lm(y ~ P*T + I(P^2) + I(T^2))
contourPlot(mod.CCD, 'P', 'T', xlim=c(-2.2, 2.2), ylim=c(-3,2))
The flow rate of distillate from the top of a distillation column.
Description
These are actual data, taken 1 minute apart in time, of the flow rate leaving the top of a continuous distillation column (data are from a 31 day period in time).
Usage
data(distillateflow)Format
A data.frame containing 44,640 observations of 1 variable
Source
Kevin Dunn, http://openmv.net
Full factorial experiments to maximize a golfer's driving distance.
Description
A full factorial experiment with four factors run by a golf enthusiast. The objective of the experiments was for the golfer to maximize her driving distance at a specific tee off location on her local golf course. The golfer considered the following factors:
-
T= Tee height (cm) -
H= Holes the golf ball had been played for prior to the experimental tee shot -
C= Club type -
D= Time of day (on the 24 hour clock)
The data are in standard order, however the actual experiments were run in random order.
Coded values for A, B, C, and D should be used in the linear
regression model analysis, with -1 representing the low value and +1 the
high value.
Usage
data(golf)Format
A data.frame containing 16 observations of 4 variables (A, B, C, D, with y as a response variable.)
Source
A MOOC on Design of Experiments: “Experimentation for Improvement”, https://learnche.org
Simulation of grocery store profits for a single product
Description
The hourly profit made when selling the product at price P and the product is displayed at height H [cm] on the shelf.
Usage
grocery(P=3.46, H=150)Arguments
P |
the selling price of the product. The default amount, if unspecified, is €3.46. |
H |
the display height of the product, as measured from the ground up. The default value, if unspecified, is 150cm. |
Details
This function simulates the hourly profit in a grocery store of selling a particular product.
Two factors can be adjusted by the user to determine the optimum:
-
P: The selling price of the product (must be a positive value). -
H: The height that the product is displayed at (must be a positive value).
Can you determine the best combination of conditions, using a systematic method (i.e. not by trial and error)?
Value
Returns the hourly profit made. Random noise is added for some realism.
Author(s)
Kevin Dunn, <kgdunn@gmail.com>
References
Please see Chapter 5 of the following book: Kevin Dunn, 2010 to 2019, Process Improvement using Data, https://learnche.org/pid
See Also
Examples
# Selling at the default settings of price (€3.46)
# and shelf height (150cm):
grocery()
# Let's try selling for a low price, €2.75,
# and put the product 120 cm off the ground
grocery(P=2.75, H=120)
# What happens if the product is too high
# for the average person?
grocery(P=1.25, H=200)
# Can you find the optimum combination of settings to
# maximize the profit, but using only a few experiments?
Simulation of a manufacturing facility's profit when varying two factors
Description
The hourly profit made when selling the product at price P and the product is produced
at a throughput rate T [parts per hour].
Usage
manufacture(P=0.75, T=325)Arguments
P |
the selling price of the product. The default amount, if unspecified, is $0.75. |
T |
the production rate (throughput), measured in parts per hour. The default value, if unspecified, is 325 parts per hour. |
Details
This function simulates the hourly profit in a manufacturing facility.
Two factors can be adjusted by the user to determine the optimum:
-
P: The selling price of the product (must be a positive value). -
T: The production rate, also called throughput (must be a positive value).
Can you determine the best combination of conditions, using a systematic method (i.e. not by trial and error)? More defects are created when production rates are too high.
Value
Returns the hourly profit made. Random noise is added for some realism.
Author(s)
Kevin Dunn, <kgdunn@gmail.com>
References
Please see Chapter 5 of the following book: Kevin Dunn, 2010 to 2019, Process Improvement using Data, https://learnche.org/pid
See Also
Examples
# Producing at the default settings of price ($0.75)
# and throughput of 325 parts per hour:
manufacture()
# Let's try selling for a higher price, $1.05,
# and a slower throughput of 298 parts per hour:
manufacture(P=1.05, T=298)
# What happens if the product is sold too cheaply
# at high production rates?
manufacture(P=0.52, T=417)
# Can you find the optimum combination of settings to
# maximize the profit, but using only a few experiments?
Industrial designed experiment to improve the volumetric heat capacity of a product.
Description
Four materials: A, B, C and D are added in a blend to achieve a desired heat capacity, the response variable, y.
The amounts were varied in a factorial manner for the 4 materials.
The data are scaled and coded for confidentiality. All that may be disclosed is that variable C is either added ("Yes") or not added not added ("No").
Usage
data(oildoe)Format
A data.frame containing 19 observations of 5 variables (A, B, C, D, and the response, y)
Source
Kevin Dunn, data from a confidential industrial source.
Pareto plot (coefficient plot) for a factorial design model
Description
Creates a plot that shows the model coefficients from the least squares model as bars. The absolute value of the coefficients are taken. The coefficient's sign is represented by the bar colour: grey for negative and black for positive coefficients.
Usage
paretoPlot(lsmodel, xlab="Effect name", ylab="Magnitude of effect",
main="Pareto plot", legendtitle="Sign of coefficients",
negative=c("Negative", "grey"),
positive=c("Positive", "black"))Arguments
lsmodel |
a linear model object (least squares model) created by the |
xlab |
label for horizontal axis in the bar plot. |
ylab |
label for vertical axis in the bar plot. |
main |
label for the plot. |
legendtitle |
an alternative to the default legend title. |
negative |
a two-element vector, both entries must be strings, the first of which provides the name for negative bars in the legend, and the second tells which colour to plot negative bars with. The default is: c("Negative", "grey"). |
positive |
a two-element vector, both entries must be strings, the first of which provides the name for positive bars in the legend, and the second tells which colour to plot those bars with. |
Details
Typical usage is to create a generic linear model with the lm(...) command, and supply that as the input to this function.
For example, a general design of experiments with 4 factors: A, B, C, and D can be built using lsmodel <- lm(y ~ A*B*C*D), and then the 2^4=16 coefficients visualized with this function using paretoPlot(lsmodel). Since the largest magnitude coefficients are mostly of interest, the coefficient bars are shown sorted from largest to smallest absolute magnitude. The sign information is retained though with the bar's colour: grey for negative and black for positive coefficients.
The coefficients are the exact coefficients from the linear model. When the linear model is in coded units (i.e. -1 for the low level, and +1 for the high level), then the coefficients represent the change in the experiment's response variable (y), for a 2-unit (not 1-unit) change in the input variable. This interpretation of course assumes the factors are independent, which is the case in a full factorial.
Please see the reference for more details.
Value
Returns a ggplot2 object, which, by default, is shown before being returned by this function. The ggplot2 object may be further manipulated, if desired.
Author(s)
Kevin Dunn, <kgdunn@gmail.com>
References
A Pareto plot is similar in spirit to the Lenth plot, other than for the fact that absolute coefficients are shown. Please see Chapter 5 of the following book: Kevin Dunn, 2010 to 2019, Process Improvement using Data, https://learnche.org/pid
Examples
# 2-factor example
T <- c(-1, +1, -1, +1) # centered and scaled temperature
S <- c(-1, -1, +1, +1) # centered and scaled speed variable
y <- c(69, 60, 64, 53) # conversion, is our response variable, y
doe.model <- lm(y ~ T + S + T * S) # create a model with main effects, and interaction
paretoPlot(doe.model)
# 3-factor example
data(pollutant)
mod.full <- lm(y ~ C*T*S, data=pollutant)
paretoPlot(mod.full)
Water treatment example from BHH2, Ch 5, Question 19
Description
The data are from the first 8 rows of the pollutant water treatment example in the book by Box, Hunter and Hunter, 2nd edition, Chapter 5, Question 19.
The 3 factors (C, T, and S) are in coded units where: C: -1 is chemical brand A; +1 is chemical brand B T: -1 is 72F for treatment temperature; +1 is 100F for the temperature S: -1 is No stirring; +1 is with fast stirring
The outcome variable is: y: the pollutant amount in the discharge [lb/day].
The aim is to find treatment conditions that MINIMIZE the amount of pollutant discharged each day, where the limit is 10 lb/day.
Usage
data(pollutant)Format
A data.frame containing 8 observations of 4 variables (C, S, T and y)
Source
Box, Hunter and Hunter, 2nd edition, Chapter 5, Question 19, page 232.
References
Box, G. E. P. and Hunter, J. S. and Hunter, W. G., 2005, Statistics for Experimenters, Second edition. Wiley.
Simulation of stovetop popcorn cooking
Description
A fixed number of popcorn kernels are cooked are heated at the same temperature. This simulation returns the number of
kernels that are edible when the pot is left on the stove for a given number of T seconds.
Usage
popcorn(T=120)Arguments
T |
the number of seconds that the pot is left on the stove. The default amount, if not provided, is 120 seconds. |
Details
This function simulates the number of edible popcorn kernels that are made when cooking a fixed number of kernels at the same heat setting
for a given amount of T seconds.
Time durations less than 77 seconds are not supported. A vector (list) of time values is not permitted, since the goal is to perform sequential
experimentation to determine the optimum time, with the fewest number of function calls.
Value
Returns the number of edible popcorn kernels. Random noise is added for some realism.
Author(s)
Kevin Dunn, <kgdunn@gmail.com>
References
Please see Chapter 5 of the following book: Kevin Dunn, 2010 to 2019, Process Improvement using Data, https://learnche.org/pid
See Also
Examples
# Cooking for a very short duration is not supported.
# For example, popcorn(T=50) will fail
# Cooking from 77 seconds onwards is supported
popcorn(T=120)
# What happens if we leave the pot on the stove for too long?
popcorn(T=500)
# Can you find the optimum time to cook on the stove
# using the fewest number of function calls?
Solar panel example from BHH2, Chapter 5, page 230
Description
The data are from a solar panel simulation case study.
The original source that Box, Hunter and Hunter used is http://www.sciencedirect.com/science/article/pii/0038092X67900515
A theoretical model for a commercial system was made. A 2^4 factorial design was used (center point is not included in this dataset).
The factors are dimensionless groups (https://en.wikipedia.org/wiki/Dimensionless_quantity)
related to
A: total daily insolation,
B: the tank capacity,
C: the water flow through the absorber,
D: solar intermittency coming in.
The responses variables are
y1: collection efficiency, and
y2: the energy delivery efficiency.
The coded values for A, B, C, and D are given, with -1 representing
the low value and +1 the high value.
Usage
data(solar)Format
A data.frame containing 16 observations of 6 variables (A, B, C, D, with y1 and y2 as responses.)
Source
Box, Hunter and Hunter, 2nd edition, Chapter 5, page 230.
References
Box, G. E. P. and Hunter, J. S. and Hunter, W. G., 2005, Statistics for Experimenters, Second edition. Wiley."
A trade-off table of fractional factorial designs
Description
Creates a new plot that shows a trade-off table for fractional factorial designs.
Usage
tradeOffTable()Details
Displays the following trade-off table:
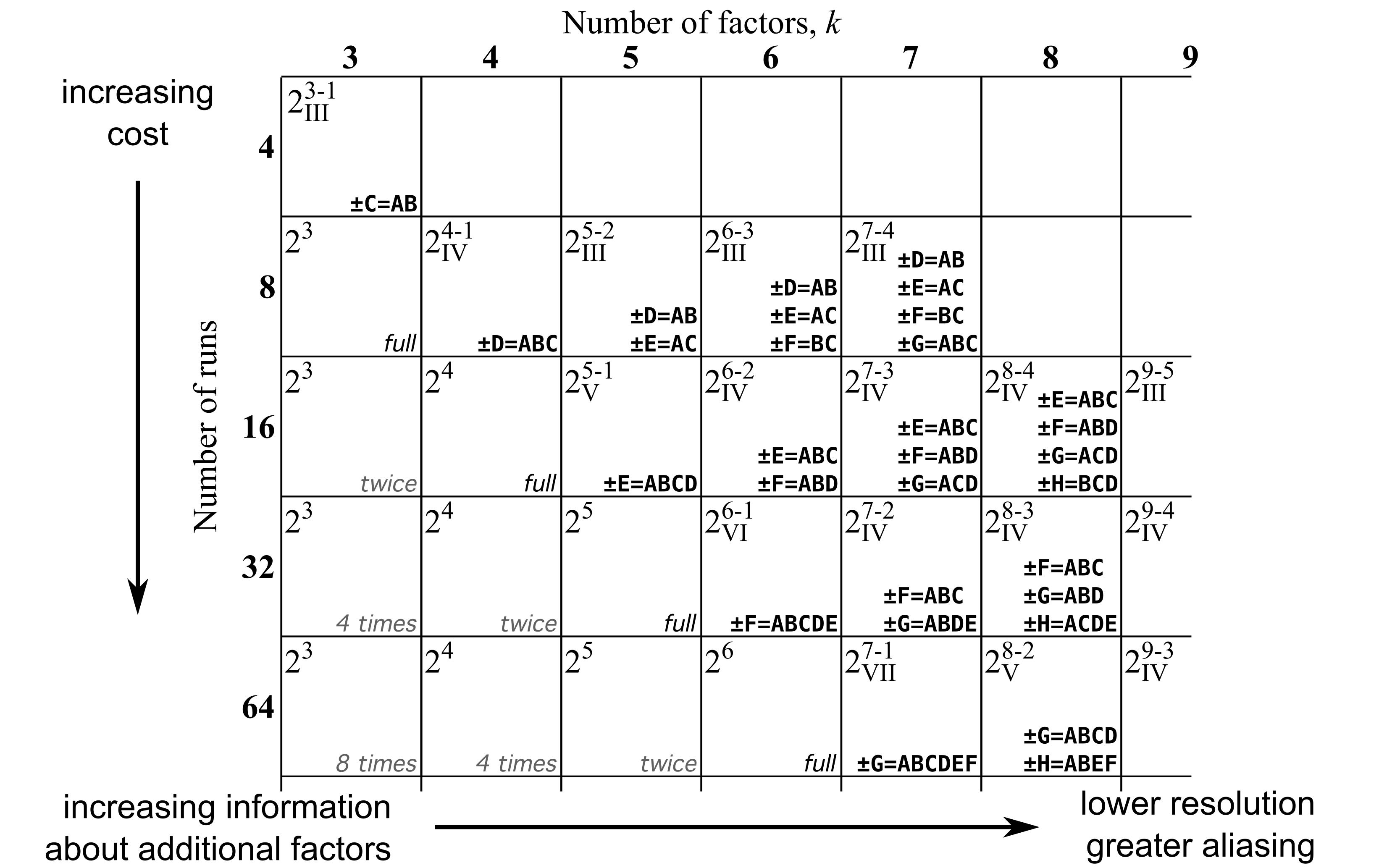
The rows in the table are the number of experiments done in the fractional factorial (n).
The columns are the number of factors under investigation in the design (k).
The cell at a particular row/column intersection gives several pieces of information:
The top-left entry of the form:
2^{k-p}=n. For example,p=1corresponds to half-fractions, andp=2corresponds to quarter-fractions.The subscript in the top-left entry, written in Roman numerals gives the design resolution. For example,
IVcorresponds to a resolution 4 design, implying 2-factor interactions are at most confounded with other 2-factor interactions.The bold entries in the bottom-right tell how to generate the remaining factors in the design.
A "full" entry indicates a full factorial; while "twice" indicates a twice replicated full factorial.
Blank entries are impossible fractional factorial combinations.
A detailed explanation of the table is provided in the book reference.
Value
Create a new plot displaying the trade-off table.
Note
Certain blocks are not unique. For example, a 2^{8-3} resolution IV design (with 32 runs and 8 factors) is shown as having +/-F = ABC, +/-G=ABD and +/-H=ACDE. But another option is +/-H=BCDE, which you might see in other software, or tables in textbooks.
Author(s)
Kevin Dunn, <kgdunn@gmail.com>
References
Chapter 5 of the following book: Kevin Dunn, 2010 to 2019, Process Improvement using Data, https://learnche.org/pid
Please see this paper to gain an understanding of how these trade-off tables are constructed:
Arthur Fries and William G. Hunter, (1980) Minimum Aberration 2^{k-p} Designs, Technometrics, 22(4), pp. 601-608, https://www.jstor.org/stable/1268198
See Also
tradeoff which can be used to extend the table out to more factors or more experiments.
Examples
tradeOffTable()
Trade-offs for a specified fractional factorial design
Description
Fractional factorial designs are a trade-off of information learned vs. the amount of work and cost (experiments) invested. This function shows which factors are confounded (confused; aliased) with each other when running a fractional factorial. The output shows the design's resolution and how to generate the fractional factorial.
Usage
tradeoff(runs=8, factors=7, display=TRUE)Arguments
runs |
the number of (unreplicated) experimental runs in the fractional factorial design. Must be a power of 2 that is 8 or higher (e.g. 8, 16, 32, 64, ...) |
factors |
the number of factors being investigated in the fractional factorial design. |
display |
will by default print the results to the screen and also returns a list containing the same information; setting this to |
Details
Fractional factorial designs require a sacrifice in the clarity of the information learned, at the benefit of performing fewer
experimental runs; thereby decreasing cost and time to run the full set of factorial experiments. See tradeOffTable for a
visual display of this concept.
For example, when running 8 experiments with 7 factors, the design resolution (clarity of estimated effects) is going to be low. This function's output indicates how the factors are aliased (confounded) with each other, so you can evaluate the use of the design before actually performing it.
The function provides 3 main sources of information: the resolution, the generators and the aliasing structure. Each one of these is described in the reference.
Aliasing is only reported to the level of the main effects and two-factor interaction (2fi, fi2). Higher level interactions are of-course
present in many fractional factorial designs, and may be calculated from the defining relationship. Future versions of this function will
return the defining relationship to assist with this.
Value
The function currently returns a list with 3 entries: the resolution, the generator(s) and the aliasing structure.
Author(s)
Kevin Dunn, <kgdunn@gmail.com>
References
Please see Chapter 5 of the following book:
Kevin Dunn, 2010 to 2019, Process Improvement using Data, https://learnche.org/pid
Please see this paper to gain an understanding of how these trade-off tables are constructed:
Arthur Fries and William G. Hunter, (1980) Minimum Aberration 2^{k-p} Designs, Technometrics, 22(4), pp. 601-608, https://www.jstor.org/stable/1268198
See Also
tradeOffTable for a visual representation of this information.
Examples
# Running 8 experiments? What are the trade-offs with 4, 5, 6, or 7 factors?
## Not run: tradeoff(runs=8, factors=4)
## Not run: tradeoff(runs=8, factors=5)
## Not run: tradeoff(runs=8, factors=6)
## Not run: tradeoff(runs=8, factors=7)
# Running 16 experiments? What are the trade-offs ?
## Not run: tradeoff(runs=16, factors=5)
## Not run: tradeoff(runs=16, factors=6)
## Not run: tradeoff(runs=16, factors=7)
## Not run: tradeoff(runs=16, factors=8)
## Not run: tradeoff(runs=16, factors=9)